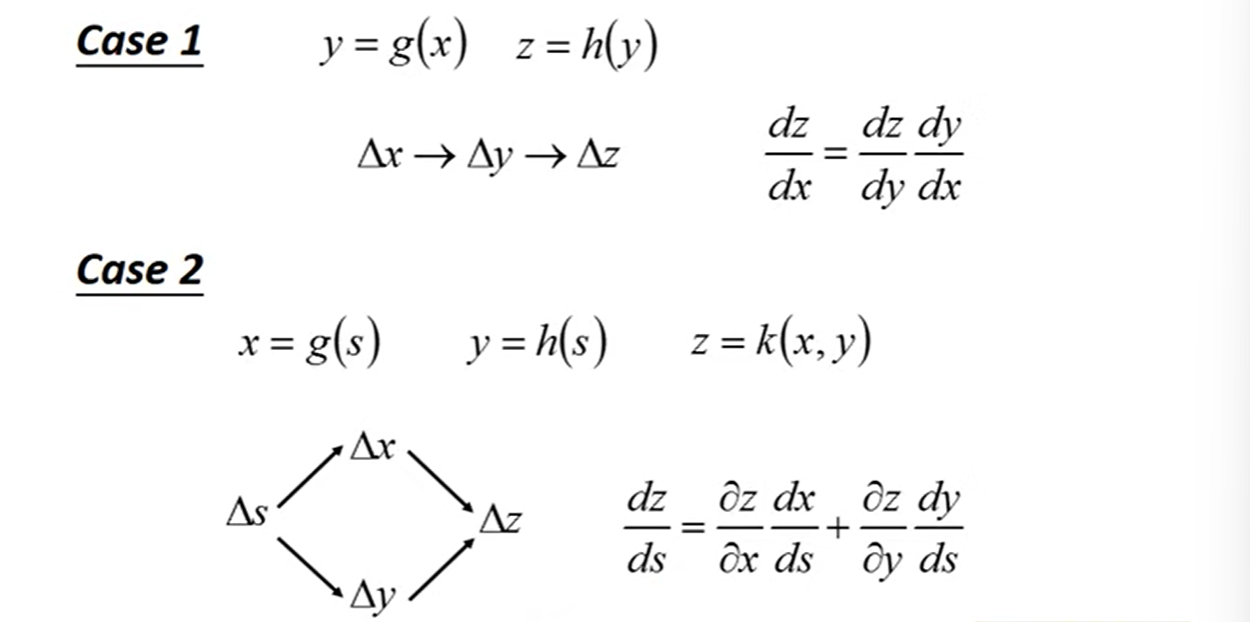1 Introduction of Deep Learning - Joooy | Zeng

Key Term:

• Machine Learning ≈ Looking for function

• Different Types of Functions

  • Regression
  • Classification
  • Structured Learning

• How to find a function

  • Step1. Function with unknow parameters
    ​ Model, weight, bias, feature
  • Step2. Define Loss from training Data
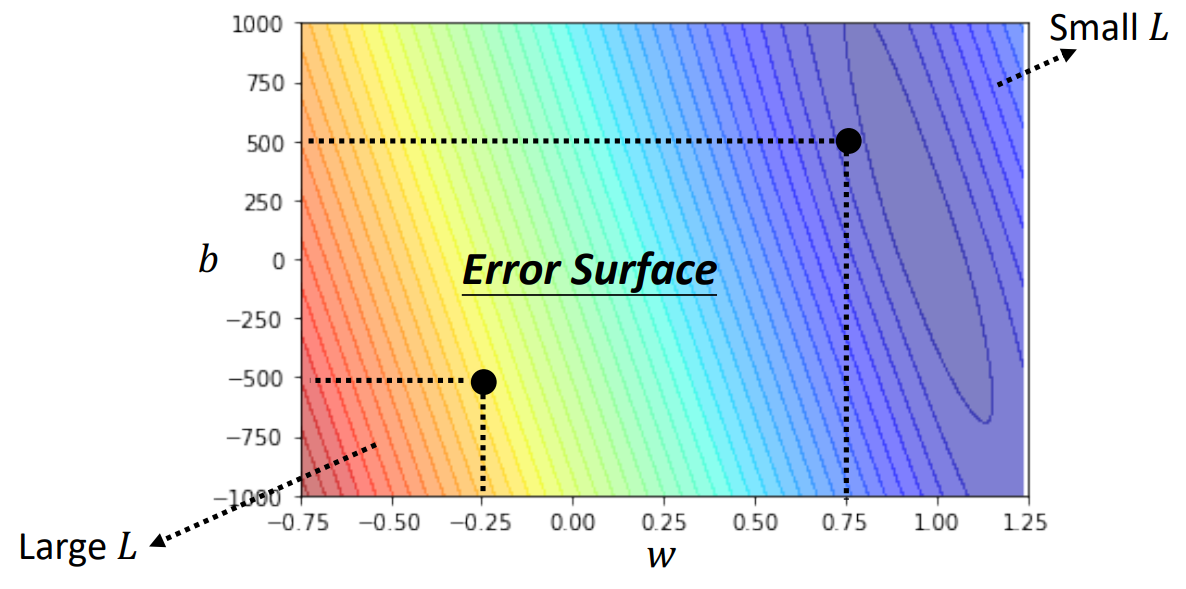
    ​ MAE, MSE, Cross-entropy, Error Surface
  • Step3. Optimization
    ​ Gradient Descent, Backpropagation Batch, Epoch

• Model
  ​ Activate Funtion

  • Linear Model
  • Sigmoid Function
  • ReLu

1 Machine Learning ≈ Looking for function

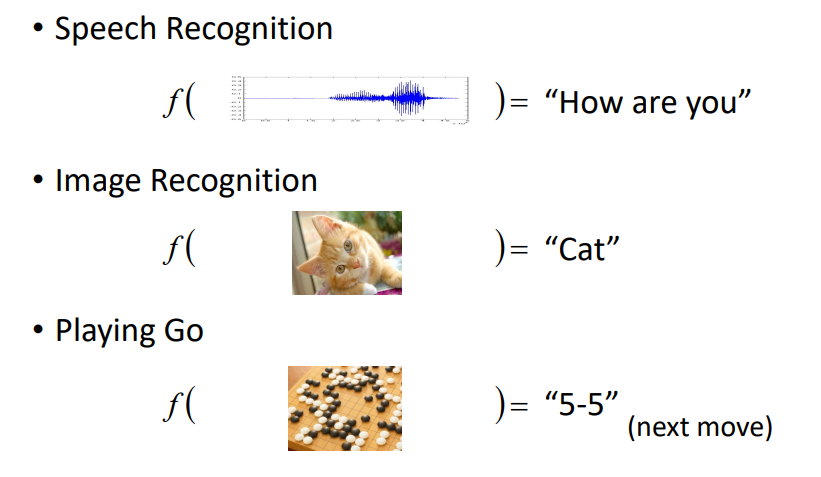
2 Different Types of Functions

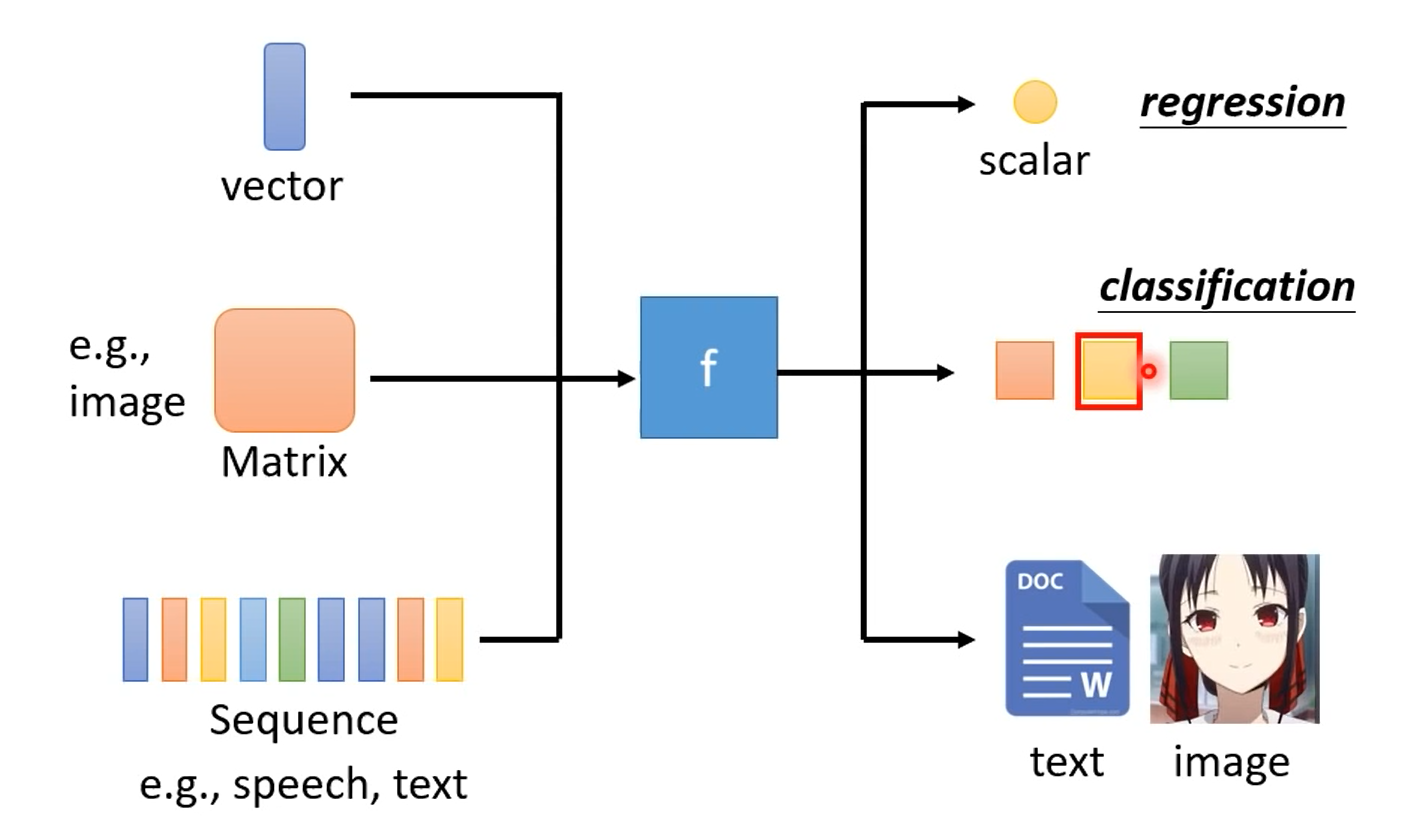
• Regression: The function outputs a scalar
• Classification: Given options (classes), the function outputs the correct one.
• Structured Learning: create something with structure (image, document)

3 How to find a function

4 ML Framework

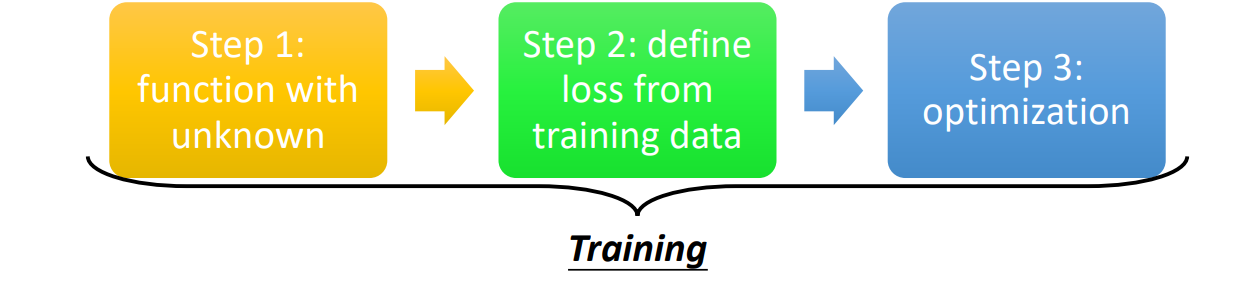
Step1. Model

How to choose: Depend on domain knowledge

Linear Models

Have model Bias (model limitation),

Sigmoid Function

Hard Sigmoid

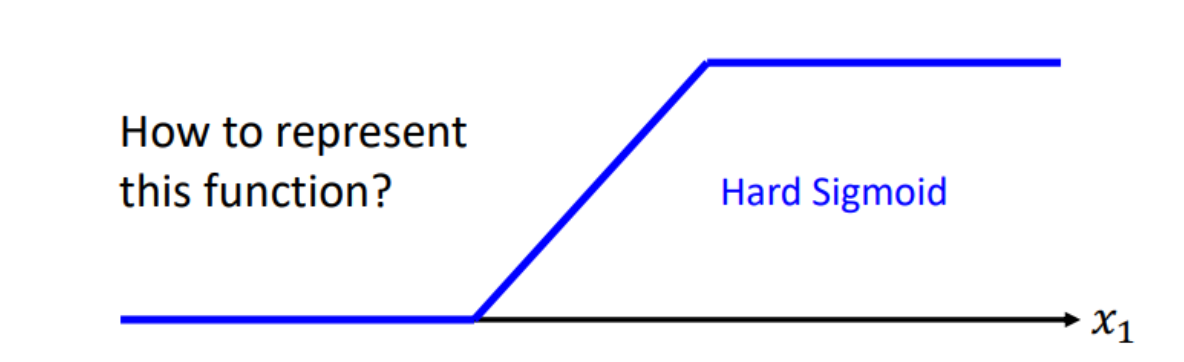
Soft Sigmoid

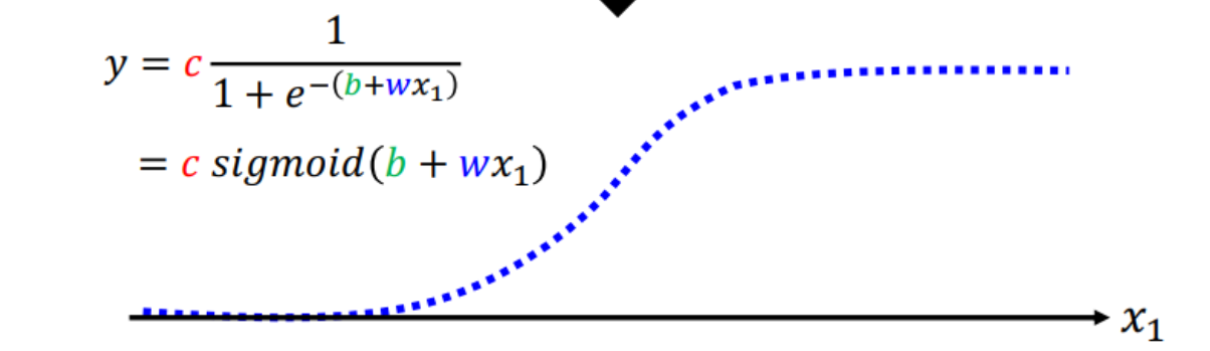
Change parameter

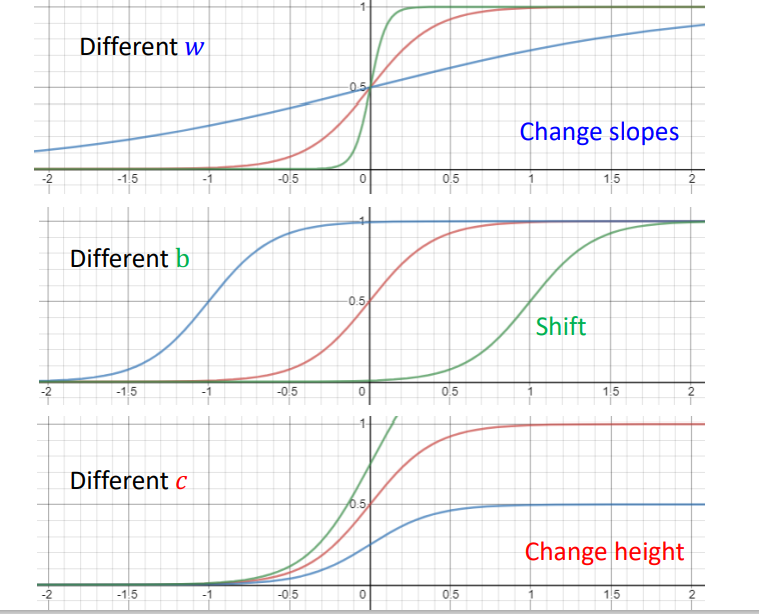
New Model: More Features

Hyperparameter:

• : no. of features
• : no. of sigmoid

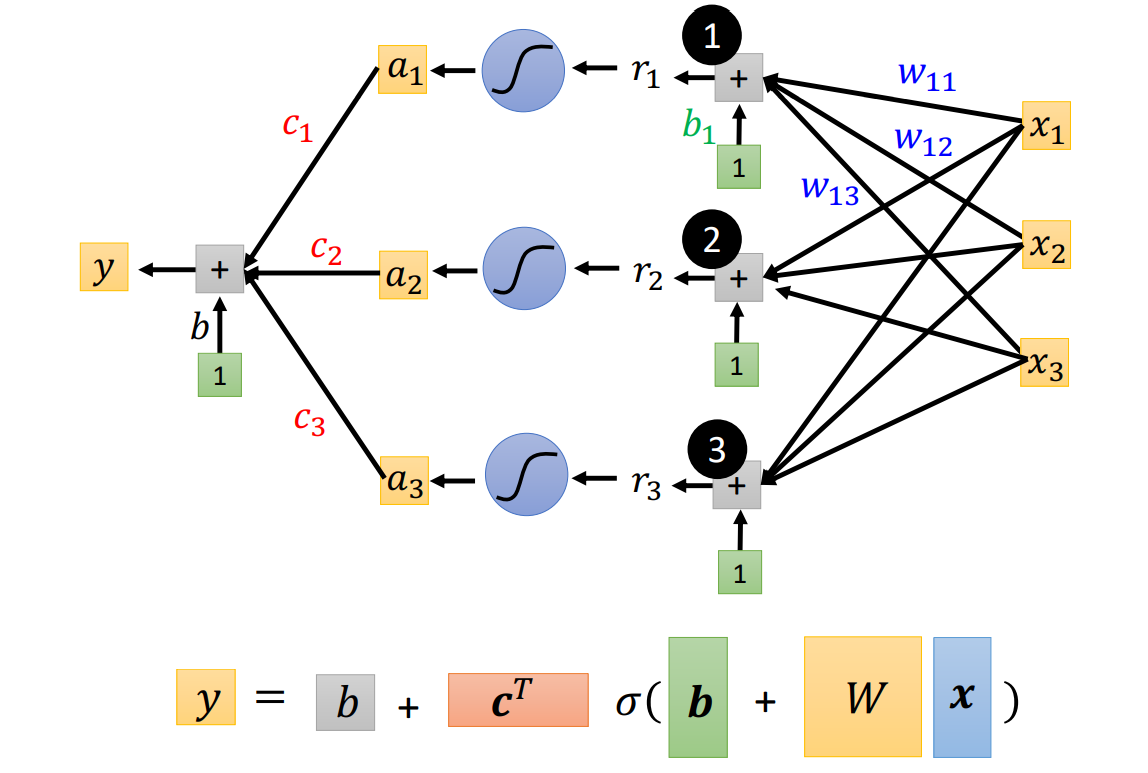
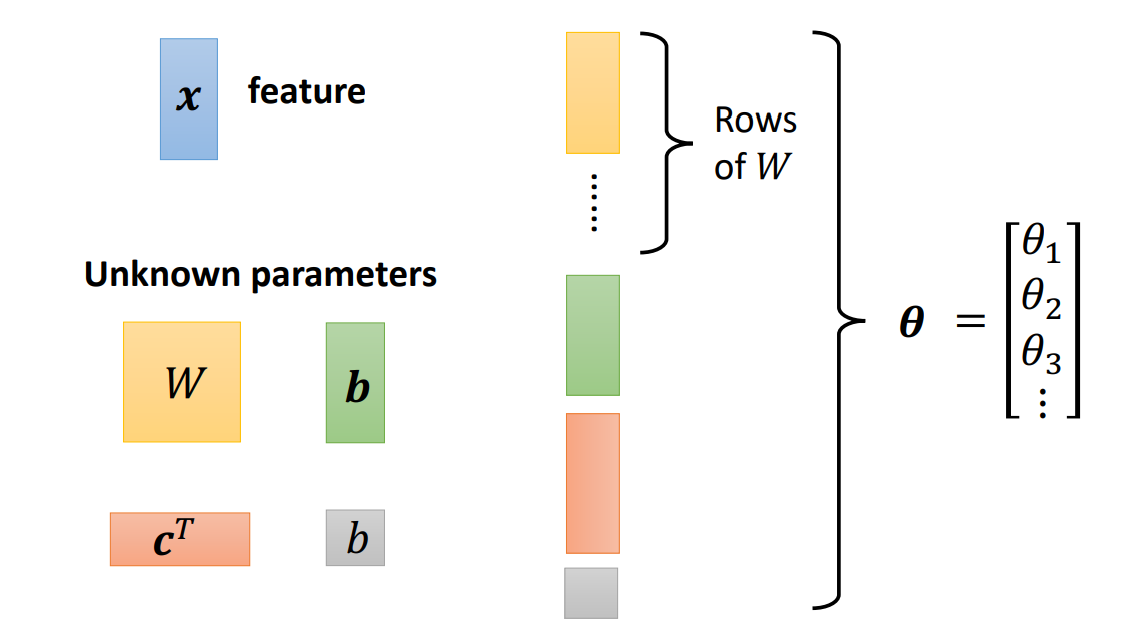
Can be seen as Matrix Operation (Why call GPU when Training)

ReLu

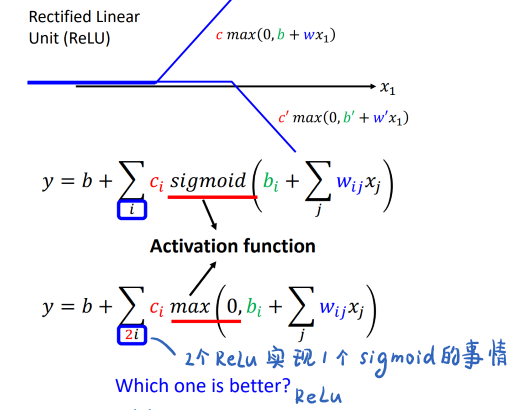
Deeper Model

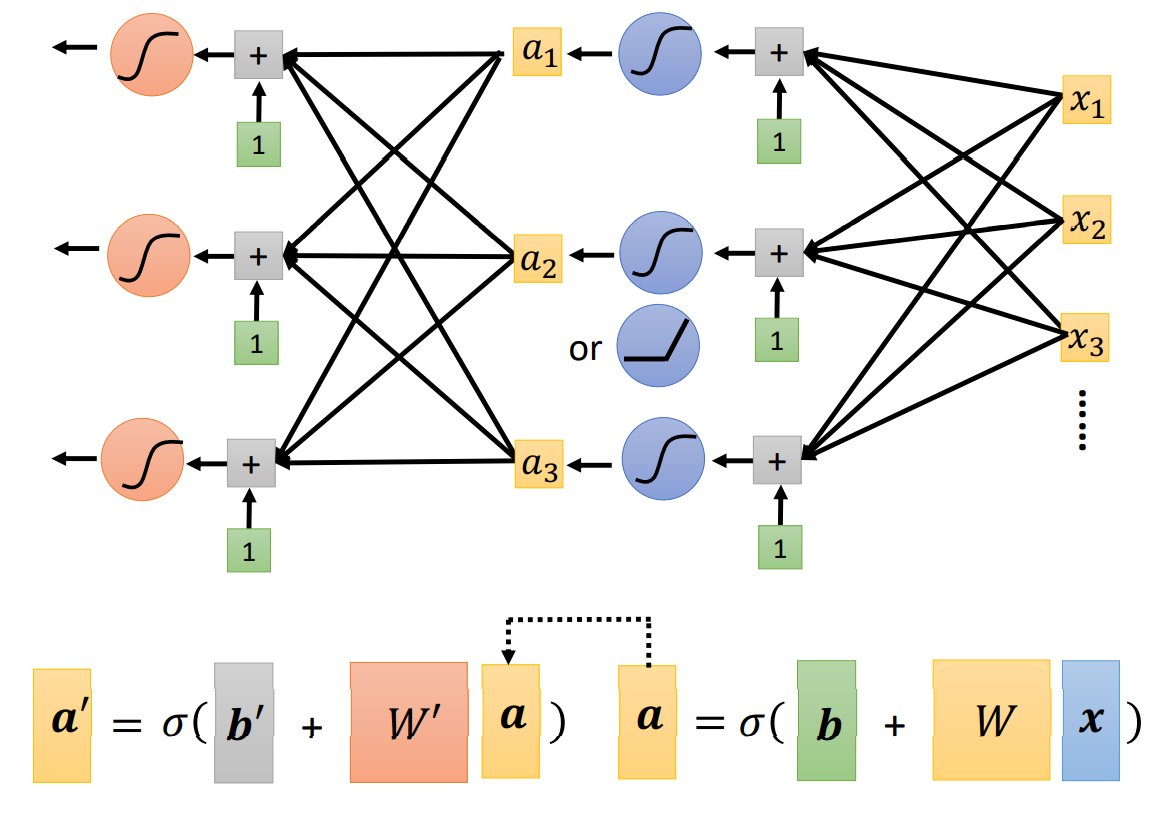
Fully Connect Feedforward Network

This is a function. Input vector, output vector.

Given network structure, define a function set.

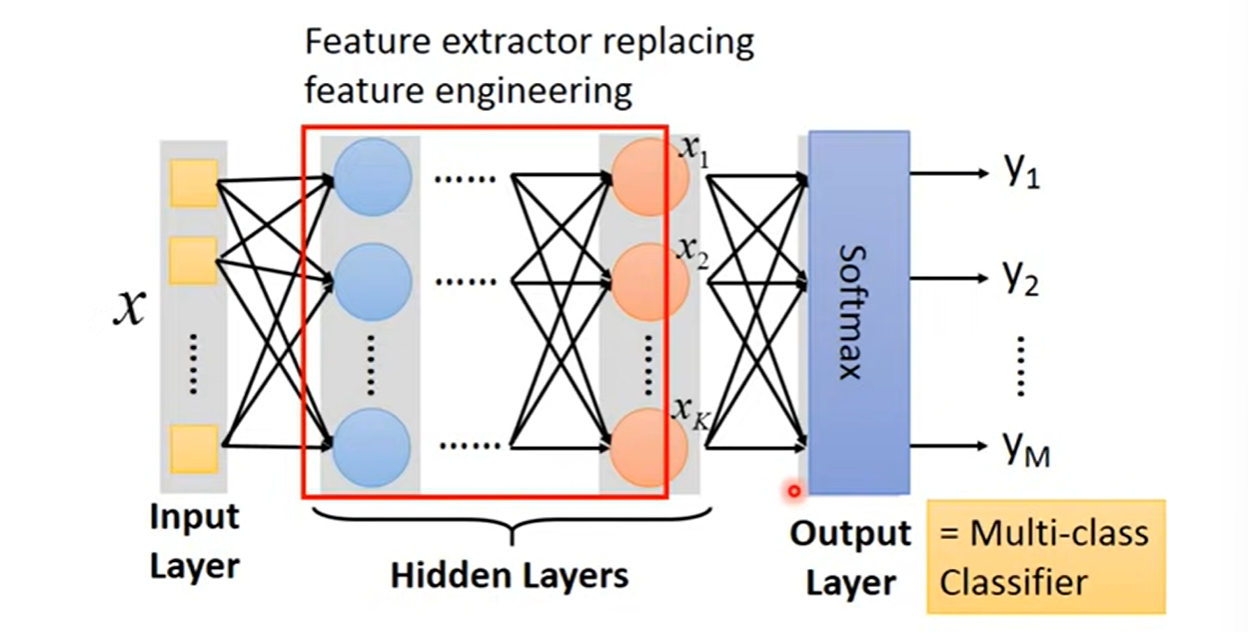
• The costum model is to do feacture engineering, which is to do feature transform to find good features.
  The deep learning does not need to find good features. It means it just use pixels. But it needs to design the structure of neural network.

• Can the structure be automatically determined?
  E.g. Evolutionary Artificial Neural Networks

Step2. Loss

• Loss is a function of parameters
• Loss means how good a set of values is.

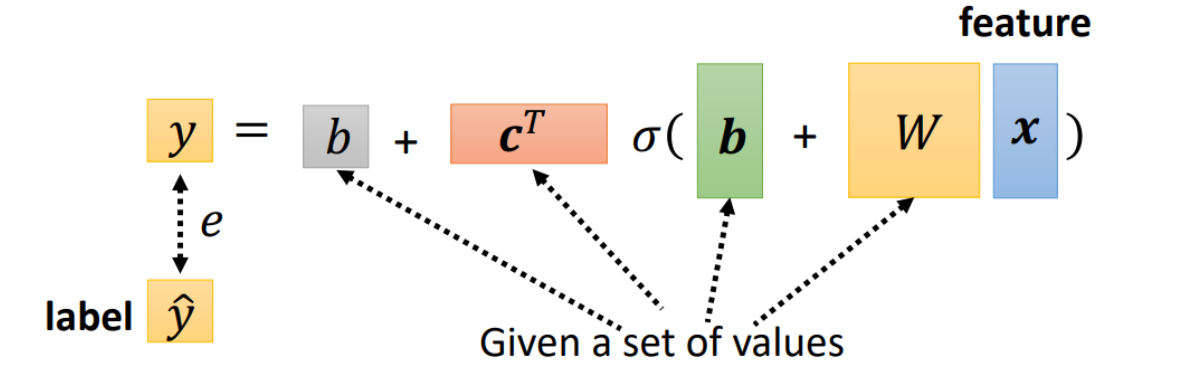
Regularization

If some noises corrupt input when testing, a smoother function has less influence.

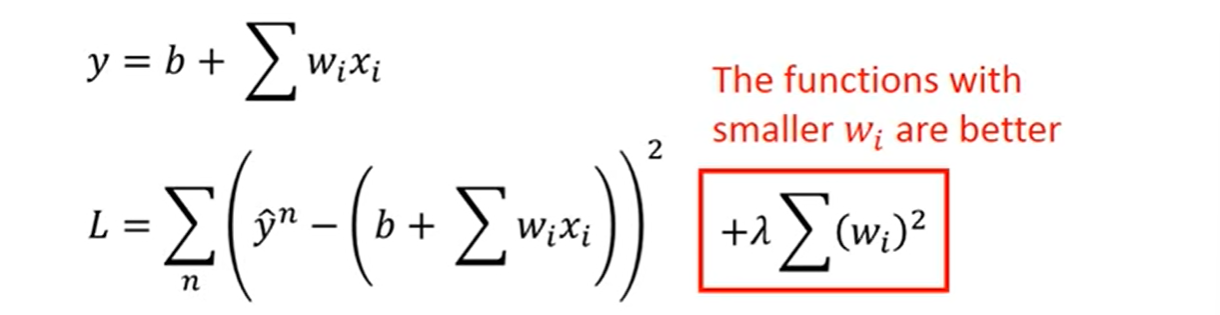
It has the better performance when we don’t consider bias on the

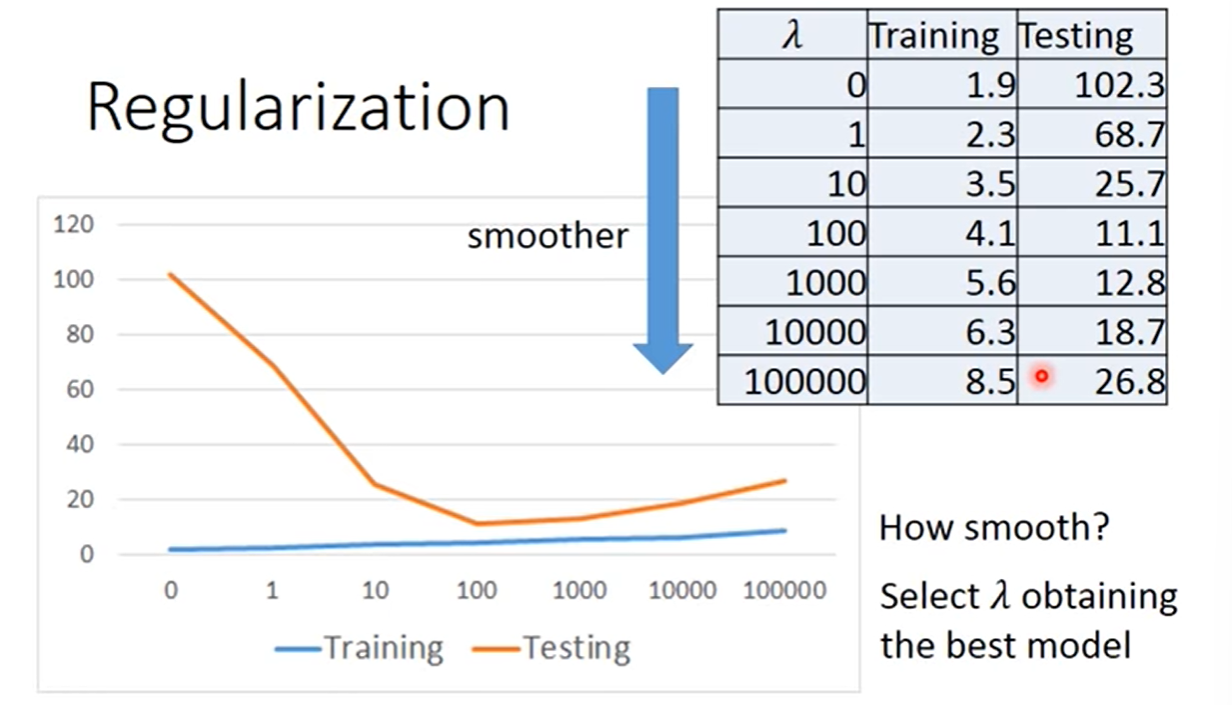
• Training erroe: larger , considering the training error less.
• We prefer smooth function, but don’t be too smooth.

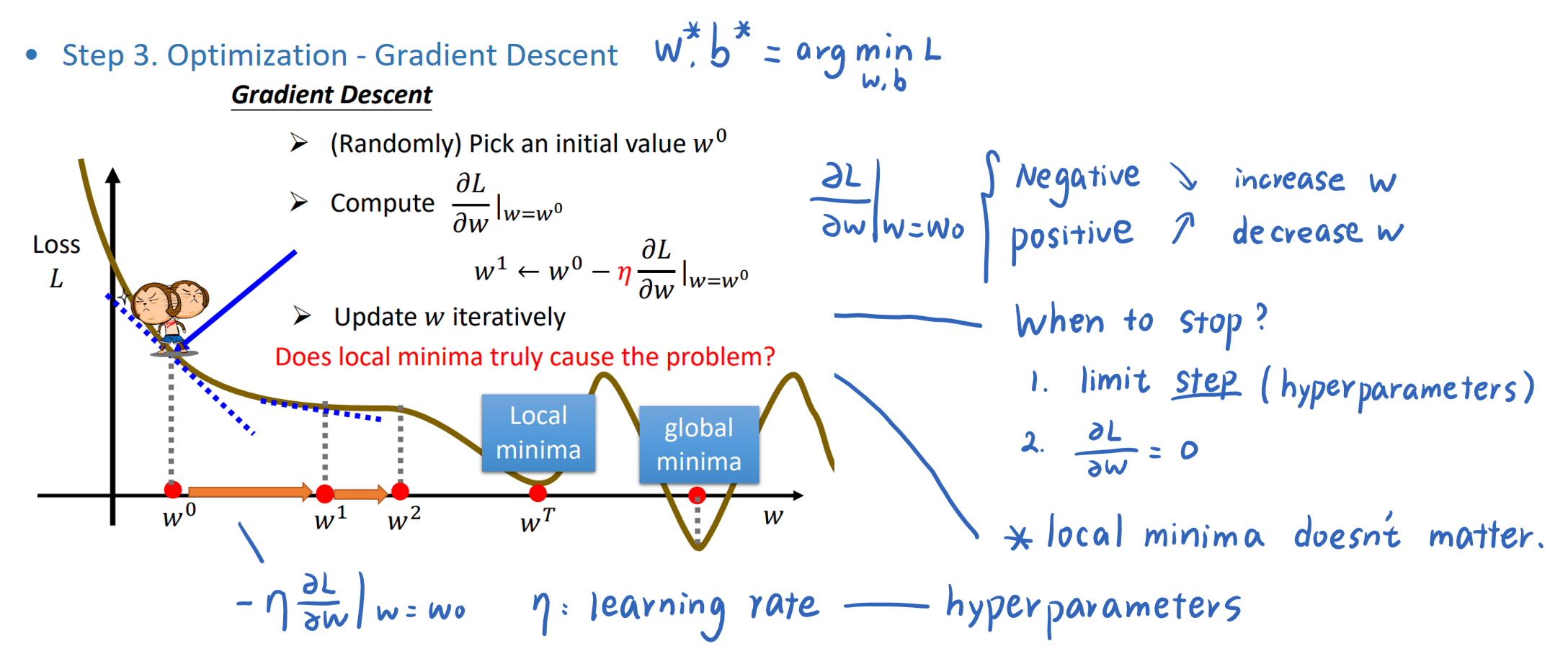
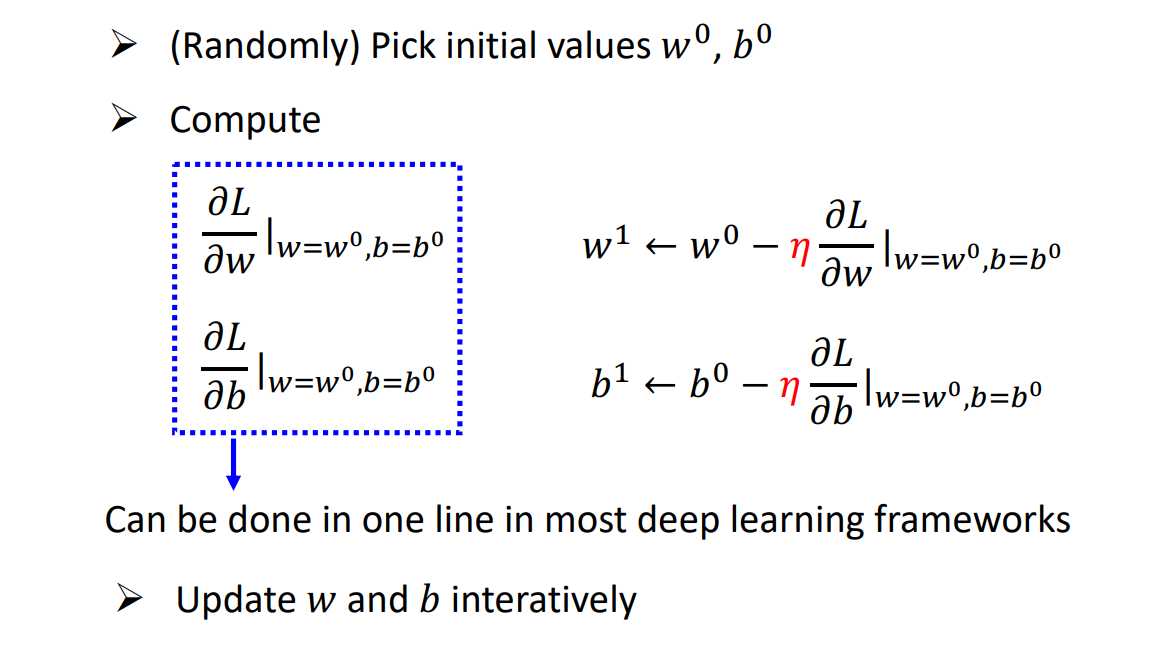
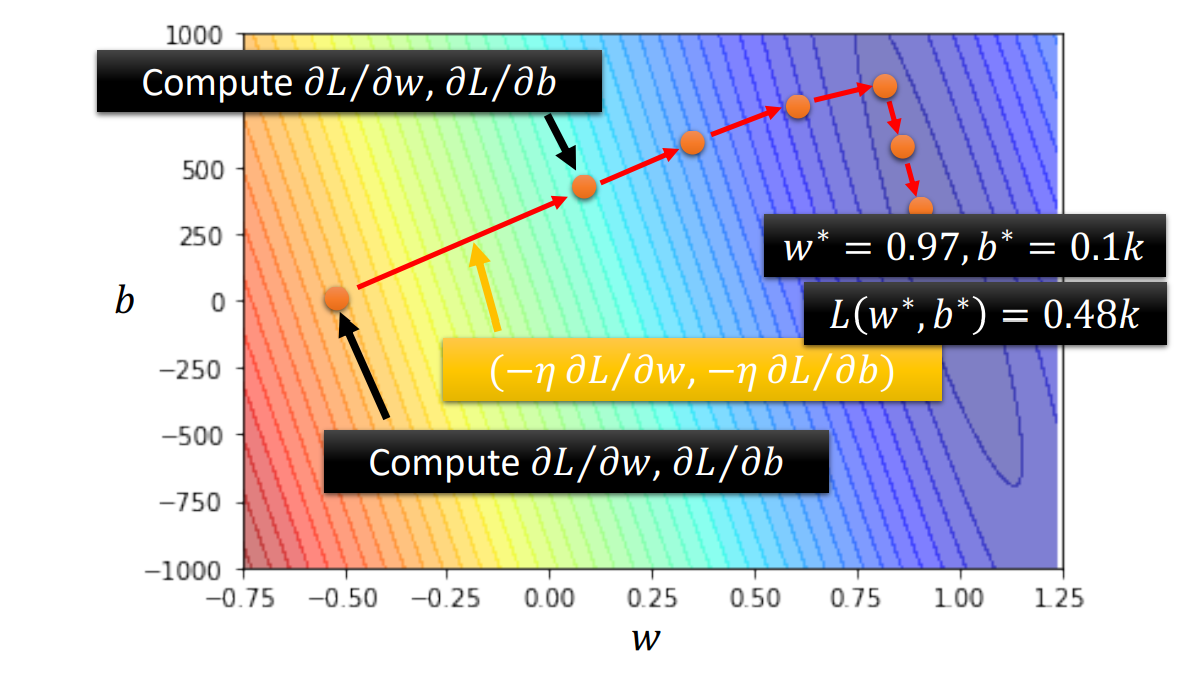
Step 3. Optimization

Optimization of New Model

Backpropogation

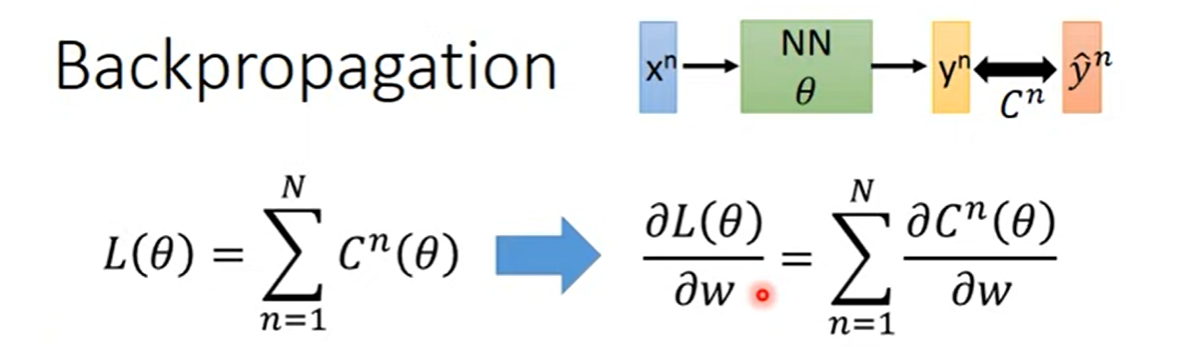
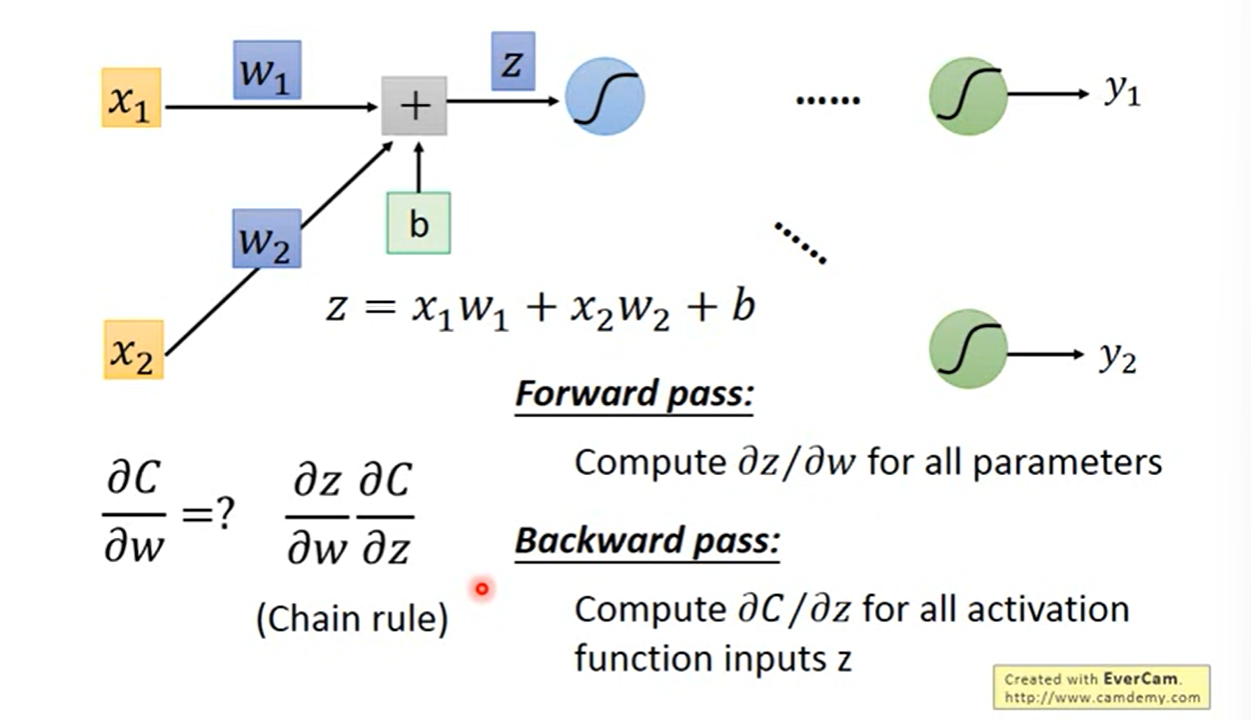
Backpropagation - Backward Pass

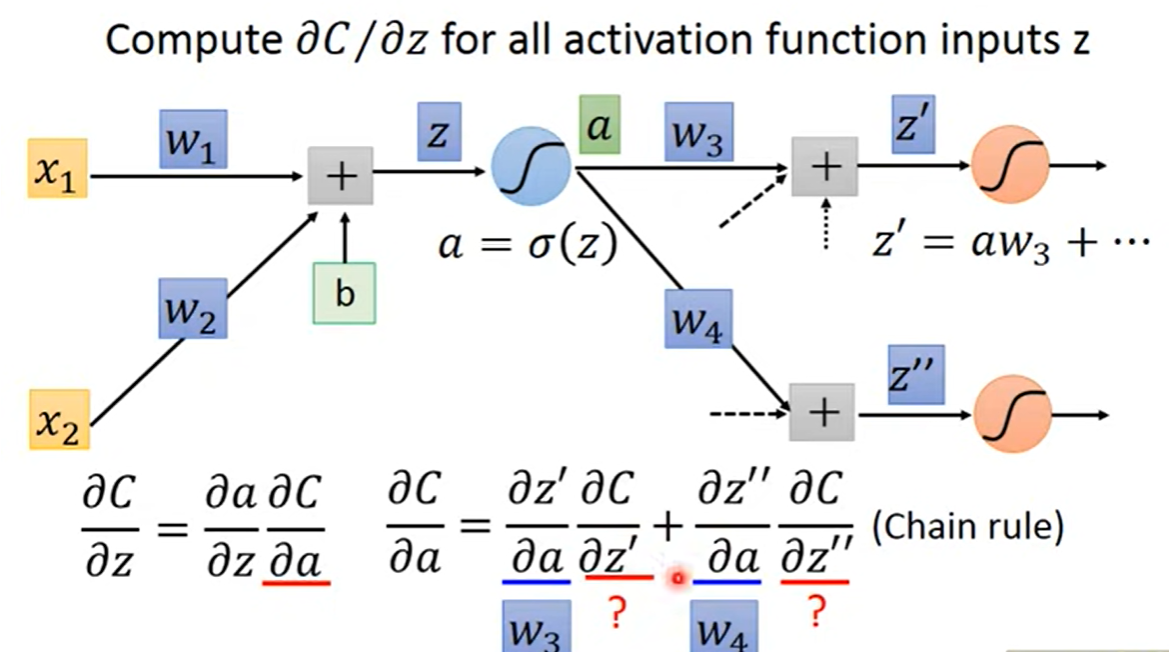
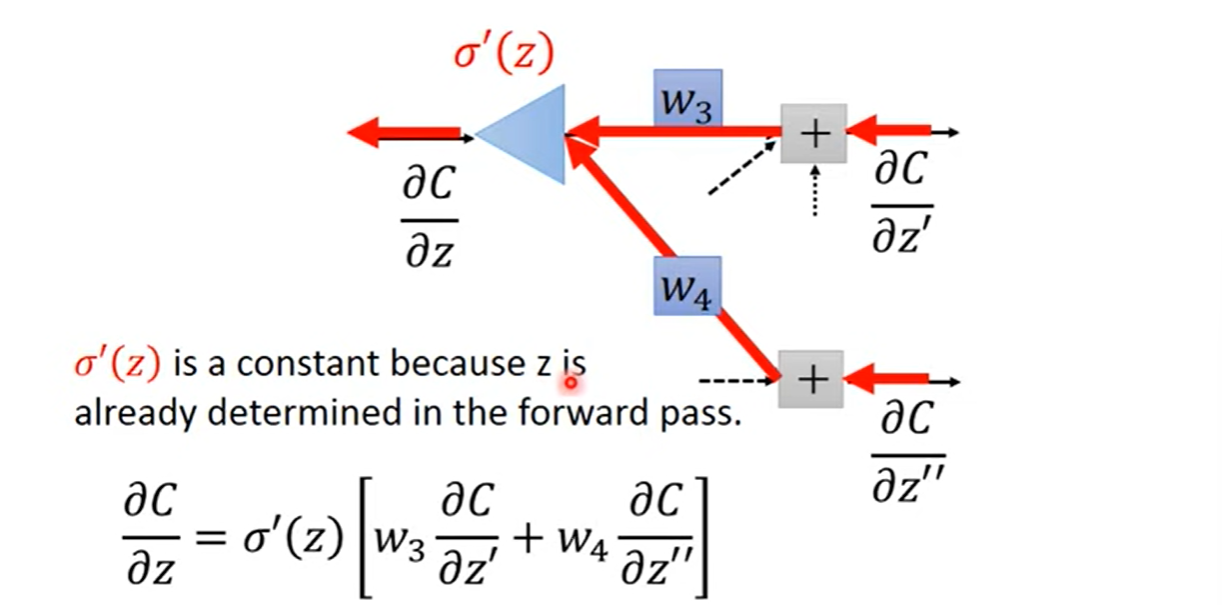
Compute recursively, until we reach the output layer.

Chain Rule

Batch & Epoch

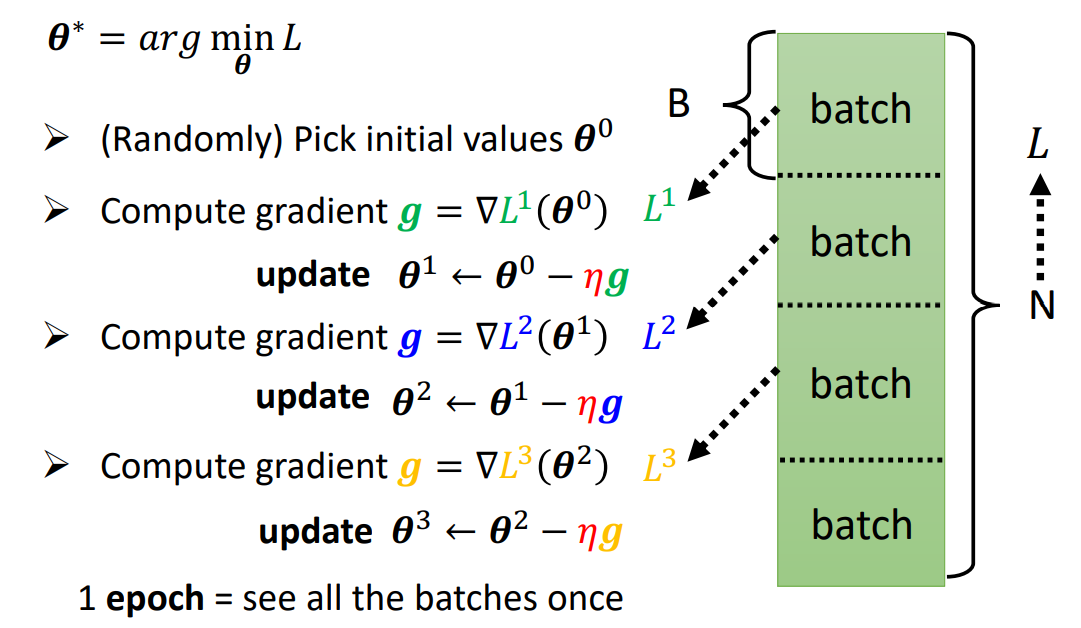
• Suppose we have 1k data, the batch size is 100,
  • so the number of update in 1 epoch will be 10.

Backpropagation

An efficient way to compute in neural network.

5 Deep Learning

• Many layers means Deep -> Deep Learning

Why don’t we go deeper?

Overfitting: Better on training data, worse on unseen data.

figure: Loss for mutiple hidden layers

5.1 History of Deep Learning