1 Key Terms
- Heuristic method
- Satisfying solution
- Genetic algorithms
- Survival of the fittest
- Genes and chromosomes
- Genetic operators (mutation and crossover)
- Population size
- Elites and offsprings
- Objective functions
2 What If There Is Not an Optimal Solution?
When the problem is too complex to be solved optimally, we use heuristic methods to solve the problem with a reasonably good (i.e., satisfying) outcome using one of the mathematical programming techniques. However, unlike mathematical programming techniques, heuristic methods will not guarantee an optimal (i.e., the best) solution; instead, a heuristic technique will use a logical method to produce a “good” solution to a highly complex problem.
3 Types of Heuristic Methods
There are many heuristic (also called metaheuristic) optimization techniques in the literature. The notable ones include Tabu Search, simulated annealing, genetic algorithms, particle swarm optimization, and ant colony optimization. As you can see from these names, most heuristic optimization techniques are modeled after some type of natural phenomenon. In this module, we explain genetic algorithms, which are arguably the most popular and most commonly used heuristic optimization techniques.
3.1 Genetic Algorithms
Genetic algorithms are a part of the family of nature-inspired global search optimization techniques. They are usually used to find approximate solutions to optimization problems that are too complex to be solved with traditional optimization methods (which, as discussed in the previous module, guarantee the best solution to a specific problem). Genetic algorithms are a part of the machine learning family of methods under artificial intelligence. They are considered a heuristic method since they cannot guarantee the optimal solution (arguably the most famous one).
Genetic algorithms are sets of computational procedures that conceptually follow the steps of the biological processes of evolution. That is, better and better solutions evolve from the previous generation of solutions until an optimal or near-optimal solution is obtained. Genetic algorithms (also known as evolutionary algorithms) demonstrate self-organization and adaptation in much the same way biological organisms do by following the chief rule of evolution, the “survival of the fittest.” The method improves the solution by producing offspring (i.e., a new collection of feasible solutions) using the best-fitted solutions of the current generation as “parents.” The generation of offspring is achieved by a reproduction process modeled after genetic reproductions, where mutation and crossover operators are used to manipulate genes in constructing newer and “better” chromosomes. (Notice that a simple analogy between [genes and decision variables] and between [chromosomes and potential solutions] underlies the genetic algorithms terminology.)
Genetic algorithms have been successfully applied to a wide range of highly complex real-world problems, including vehicle routing, bankruptcy prediction, and web searching.
3.2 The Generic Algorithm (GA) Process: How Does GA Work?
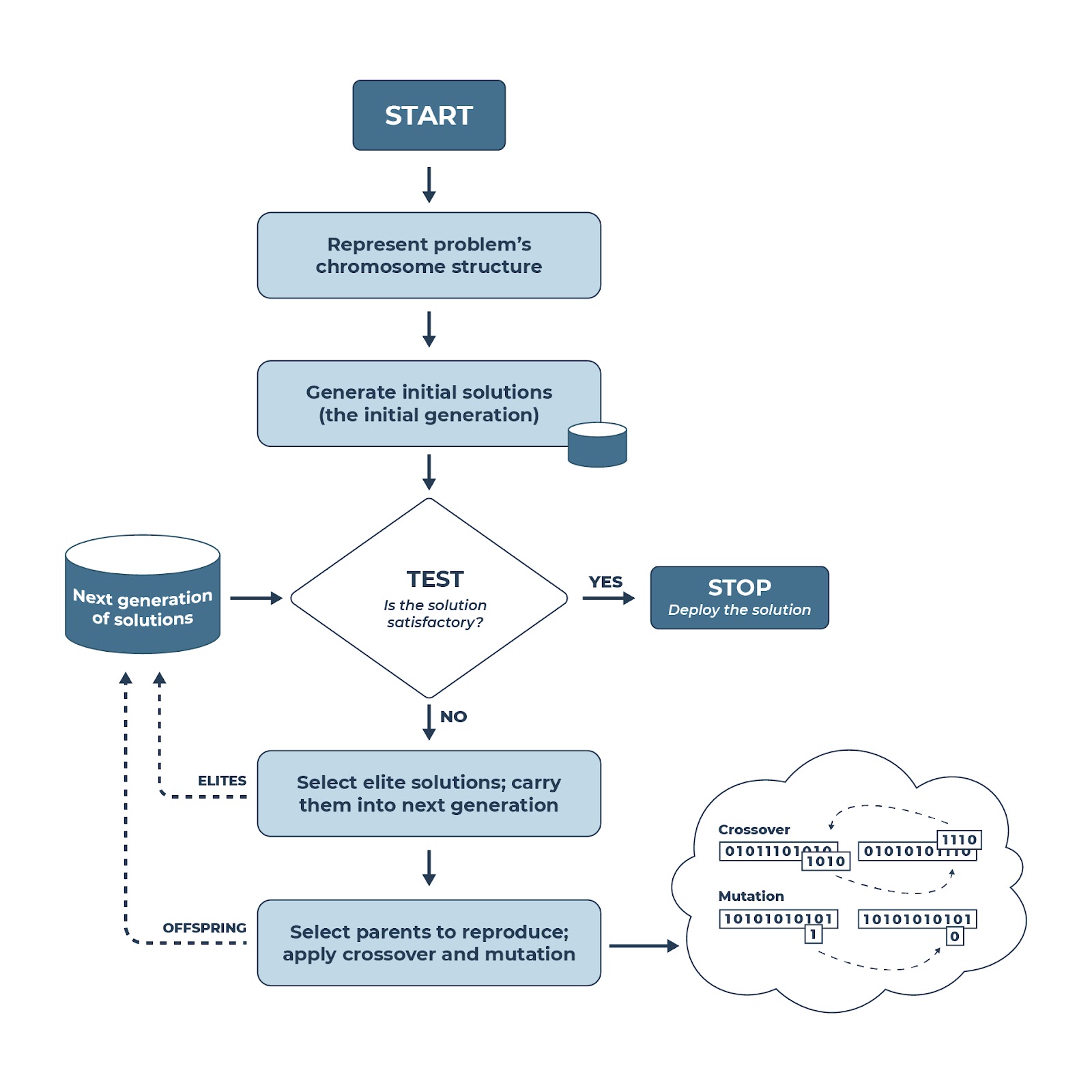
Figure 1 below shows the flow diagram of a typical genetic algorithm process. The process starts with describing and representing the problem in a manner amenable to the genetic algorithm. Typically, this means that a string of 1s and 0s (or other more recently proposed complex representations) are used to represent the decision variables. This collection represents a potential solution to the problem (analogous to individual genes that constitute chromosomes).
Figure 1: Flow diagram of a typical genetic algorithm process [*Long Description]*
Next, the decision variables are mathematically or symbolically pooled into a fitness (or objective) function. The fitness function can be one of two types: maximization (i.e., something that is “more” is better, such as profit) or minimization (i.e., something that is “less” is better, such as cost). Along with the fitness function, you should also represent all of the constraints on decision variables that collectively dictate whether a solution is feasible. Remember that only the possible solutions can be a part of the solution population. Infeasible ones are filtered out before finalizing a generation of solutions in the iterations process.
Once the representation is done, an initial set of solutions (i.e., the initial population) is generated, all infeasible solutions are eliminated, and the fitness functions of feasible ones are computed. The solutions are ranked-ordered based on their fitness values, so those with better fitness values are given more probability (proportional to their relative fitness value) in the random selection process.