Prescriptive Analytics
March 13, 2023

7 Multi-Criteria Decision Modeling

1 Introduction

Sometimes, if you are lucky, or if you can simplify the problem situation, you may have a straightforward decision-making condition characterized by a single goal, a limited and clearly identifiable number of alternatives, and a single, easily measurable, and quantifiable criterion. However, in most real-world situations in personal or professional contexts, you will face decision choices characterized by many (and often conflicting) goals, many (sometimes virtually unlimited) alternatives, and numerous criteria. Making rational (i.e., optimal or near-optimal) decisions in such complex situations requires the use of scientific methods to identify the “optimal” decision without making unrealistic, overly-simplified assumptions. A family of scientific methods, commonly called multi-criteria decision-making methods, can help you address these complex decision situations.

2 Key Terms

3 Real Decisions Involve Multiple Criteria and Multiple Objectives

Many real-world decisions involve multiple criteria and multiple objectives. In a business context, these decisions include supplier selection, product mix optimization, financial sourcing, location identification, and crew or job scheduling, among others. In a personal context, these decisions may include purchasing a house or car, deciding on a graduate school, retirement planning, etc. In other words, life involves a wide variety of personal and professional decision-making situations. At the highest level of conceptualization, these decisions can be grouped into four types:

  1. The choice problem. The goal is to select the single best option or reduce the group of options to a subset of equivalent or incomparably ‘good’ options. An example of this would be a manager selecting the right person for a particular project.
  2. The sorting and grouping problem. Here, options are sorted into ordered and predefined groups or categories. The aim is to regroup the alternatives that share similar behaviors or characteristics for descriptive, organizational, or predictive reasons. For instance, employees can be evaluated for classification into different categories such as ‘outperforming employees,’ ‘average-performing employees,’ or ‘weak-performing employees.’ Based on these classifications, necessary measures can be taken. Sorting methods are appropriate for repetitive or automated use. They can also be used for initial screening to reduce the number of options that would need to be considered in a subsequent step.
  3. The ranking problem. Options are ordered from best to worst using scores, pairwise comparisons, etc. The order of options can be either partial (if incomparable options are considered) or complete. A typical example of this is the ranking of universities using several criteria, such as teaching quality, research expertise, career opportunities, etc.
  4. The description problem. The goal is to describe options and their consequences, and this is usually done as a first step towards understanding the characteristics of a decision problem.

The decision sciences community also proposed other decision types, but they are primarily derivatives of the ones mentioned above. These other types include the elimination problem (a particular branch of the sorting problem) and the design problem (where the goal is to identify or create a new action that will meet the goals and aspirations of the decision maker).

4 Characteristics of Typical Multi-Criteria Decisions

Real-world decisions are usually complex, and the human brain cannot objectively solve such complex problems. Therefore, we often make assumptions (often unrealistic assumptions) to eliminate the majority of objectives or attributes/criteria so that the problem becomes simple enough to solve. (This is an intrinsic outcome of “bounded rationality” in humans.) This will typically lead to a far less optimal solution to the underlying real and complex problem.

An alternative to this condition is to rely on scientific or mathematical methods that can help impose structure into decision situations. Such an approach can better deal with the complexity posed by the problem. There are a vast number of mathematical and scientific methods that have been developed to better deal with complex decision problems, and there is a fundamental reason for such an extensive collection of methods. This is because each problem situation has unique features that make it more effectively and efficiently solvable with a specific method that can address it better than other methods. Hence, over time, various methods have been developed to address these unique situations, which in the end has led to a rich collection of heuristic decision analysis methods and methodologies.

5 Types of Multi-Criteria Decision Modeling (MCDM) Methods

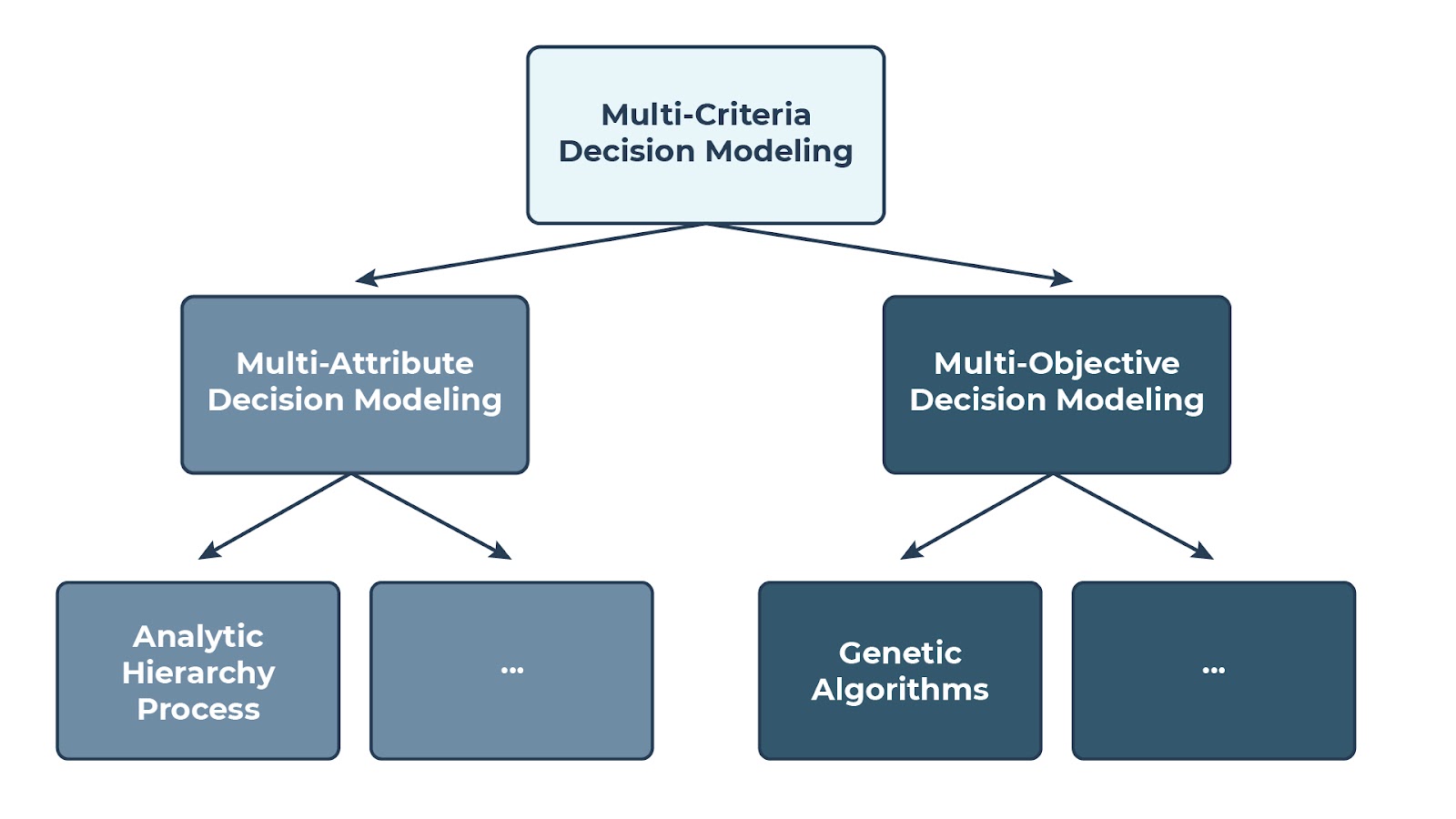
Figure 1 below presents a simple taxonomy to better understand the landscape of mathematical/scientific solution methods that were developed to deal with complex decision problems. These are usually called multi-criteria decision modeling (MCDM) methods.

At the highest level, MCDM methods can be grouped into two main categories: multi-attribute decision-making (MADM) and multi-objective decision-making (MODM).

Shows the make up of multi-criteria decision modeling (MCDM). There is a text box at the top containing the phrase "multi-criteria decision modeling." There are arrows pointing from this box to two other text boxes below, one on the left containing the phrase "multi-attribute decision modeling" or MACM, and one on the right containing the phrase "multi-objective decision modeling" or MODM. From the MADM box, another two arrows point to text boxes below, on the left containing the phrase "analytic hierarchy process" but the right text box is blank. From the MODM text box, two arrows proceed to two other boxes below, on the left to one containing the phrase "genetic algorithms," and again, the right side box is blank.

Figure 1: A simple taxonomy for MCDM methods

5.1 MODM Methods

MODM methods study decision problems where the decision space is continuous and where there can be numerous, and often an infinite number of, alternatives or potential solutions. Typical examples of problems that fall under MODM methods are mathematical programming and constraint-optimization problems, potentially with multiple and conflicting objective functions. In general, MODM methods have decision variables, the values of which are determined within a continuous or integer domain and presented as either an infinitive or a vast number of alternative choices. The best choices should satisfy the constraints while producing the best value for the decision maker’s objective function (i.e., the goal). A simplified version of MODM problems can be solved with the linear/nonlinear programming or genetic algorithm-based optimization methods that we covered in the previous modules.

5.2 MADM Methods

MADM methods have widespread application. Although there are a large and diverse number of MADM methods, many share common features, including the goal, alternatives, attributes (or criteria), decision weights, and decision matrix. Let’s consider each of these.

5.2.1 Goal

The goal is to select the best alternative while collectively considering all attributes in the problem space. Attributes may conflict with each other since they represent different criteria dimensions of the alternatives. For example, the cost of “quality” may conflict with “the profit from sales.”

5.2.2. Alternatives

Alternatives represent the different choices or feasible options for action available to the decision maker. Usually, the set of alternatives is assumed to be finite, ranging from several to even hundreds. They are supposed to be screened, prioritized, and eventually ranked.

5.2.3 Attributes

Attributes are criteria for making decisions, and each MADM problem contains multiple attributes. Attributes represent the different dimensions from which you can view alternatives. In cases where there are many attributes, they may be arranged in hierarchical groups for better structuring and representation. In such cases, some attributes may be considered “major” attributes and may each be associated with several sub-attributes. Similarly, each sub-attribute may also be associated with several sub-sub-attributes and so on. Although some MADM methods may explicitly consider a problem’s hierarchical structure of the attributes, most methods assume a single level of attributes (i.e., no hierarchical structure).

Another issue arises when there are incompatible attribute measures since different attributes may use other units of measurement. For instance, in buying a used car, the attribute cost may be measured in terms of dollars, and mileage may be measured in terms of thousands of miles. Having to consider these different units of measurement can make a MADM an intrinsically more complex problem to formulate and solve without the help of scientific/mathematical methodology.

5.2.4 Decision Weights

Decision weights are the relative importance given to problem attributes, and most MADM methods require that weights of importance are assigned to attributes. Usually, these weights are normalized to add up to “1.” These weights are generally determined by a specific procedure depending upon the MADM method used.

5.2.5 Decision Matrix

A decision matrix is a tabular representation of all decision parameters, and MADM problems can typically be easily expressed in a two-dimensional matrix. A decision matrix A is an (M × N) matrix in which element aij indicates the performance of alternative Ai when it is evaluated in terms of decision criterion Cj, (for i = 1, 2, 3,…, M, and j = 1, 2, 3,…, N). It is assumed that the decision maker has determined the weights of the relative performance of the decision criteria (denoted as Wj, for j = 1, 2, 3,…, N). This information can best be summarized as in the following decision matrix (see Table 1).

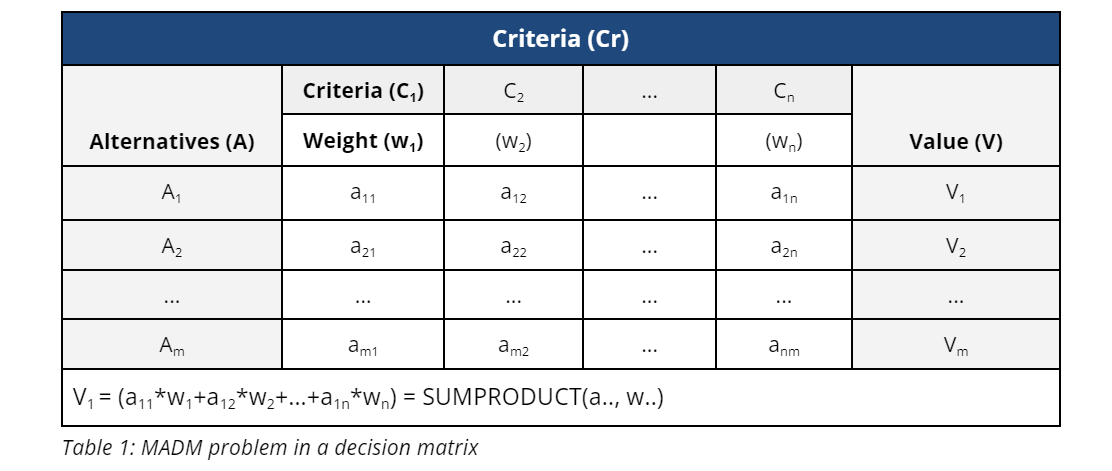
image-20230313133710179

Table 1: MADM problem in a decision matrix

Given the previous definitions, the general MADM problem can be defined as follows: A represents the set of decision alternatives, C represents the criteria, and W represents the weights of the criteria. The goal is to determine the optimal alternative A* with the highest degree of desirability related to the goal/objective.

5.3 Utility Function Analytics

To illustrate the application of the decision matrix presented in the above table, let us consider one of the simplest MADM methods, known as the weighted sum model. (It is also called the factor rating method in some operations management literature.)

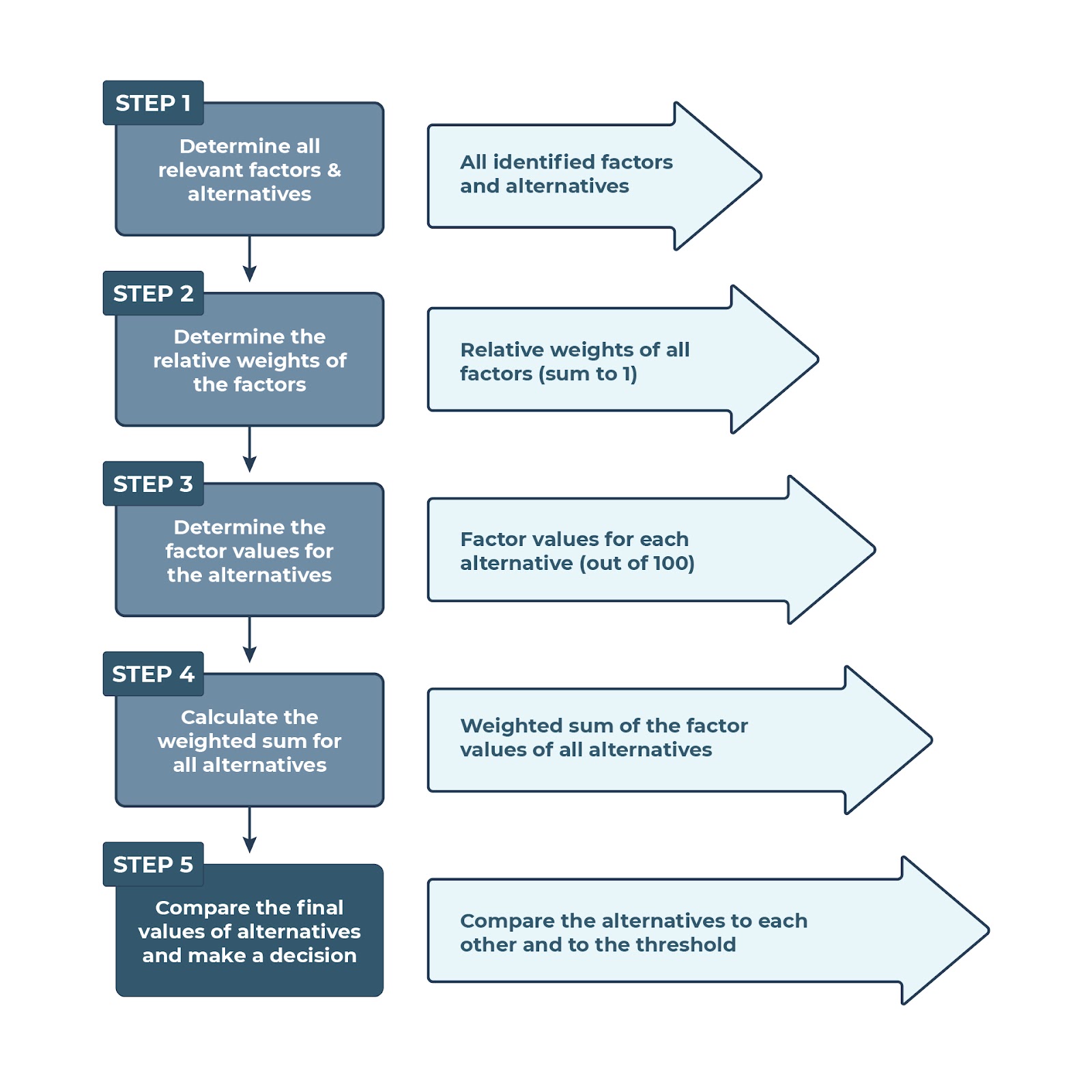
Due in large part to its simplicity and ease of operationalizability (often using spreadsheet software like Microsoft Excel), the weighted sum model is probably the most commonly used approach for the analysis of relatively small multi-criteria decision problems. Figure 2 shows the simple five-step process while executing factor-rating type decision-making.

Shows a 5-step process. For a complete description, see the long description link on the table's caption.

Figure 2: A simple process flow for the factor rating method [*Long Description]*

Under this method, if there are M alternatives and N criteria, then the solution is the alternative that best satisfies (either maximizes or minimizes, depending on the goal) the decision situation. The assumption that governs this model is the additive utility assumption, i.e., the total value of each alternative is equal to the sum of products of all alternatives and weights. In single-dimensional cases, where all the units are the same (e.g., dollars, feet, seconds), this method can be used without much difficulty.

5.4 Analytic Hierarchy Process (AHP)

Second only to the factor rating method, the analytic hierarchy process (AHP) is one of the most popular and commonly used multi-criteria decision analysis techniques. It is a theoretically (better) justified, logical, and mathematical model that takes advantage of the divide-and-conquer approach.

Professor Thomas L. Saaty developed AHP in the 1970s, and it has been extensively studied and refined by many researchers since then. Essentially, AHP is a hierarchical problem-structured technique capable of organizing and analyzing complex (multi-attribute/multi-objective) decisions based on mathematical theories and relatively simple algorithms.

Using a hierarchical structuring technique, AHP simplifies complex decisions into manageable smaller sub-decisions and uncomplicated comparisons. In other words, AHP employs the divide-and-conquer philosophy to bring order and simplicity to complicated multi-faceted decision situations. Because of its effectiveness and ease of use, AHP has been successfully deployed to address complex decision situations in various application domains, including healthcare, energy, telecom, marketing, finance, science, government, and education. Instead of prescribing the “best” solutions to a decision situation (which is often the case in optimization methods such as linear programming), AHP helps decision makers identify the decisions or solutions that best suit their goal and understanding of the specifics of the problem.

AHP provides a holistic and rational framework for:

# DS